7. 堆
定义
堆是一种特殊的树，首先，它是一个完全二叉树，其次它的每个节点的值都必须大于（或小于等于）其子节点的值。对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。
堆的实现
堆是一颗完全二叉树，所以优先使用数组存储，相比与链表法可以更节省存储空间。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。值得一提的是堆顶元素的删除操作，为了避免出现数组空洞，我们把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。堆中比较重要的两个操作是插入一个数据和删除堆顶元素。这两个操作都要用到堆化。插入一个数据的时候，我们把新插入的数据放到数组的最后，然后从下往上堆化；删除堆顶数据的时候，我们把数组中的最后一个元素放到堆顶，然后从上往下堆化。这两个操作时间复杂度都是 O(logn)。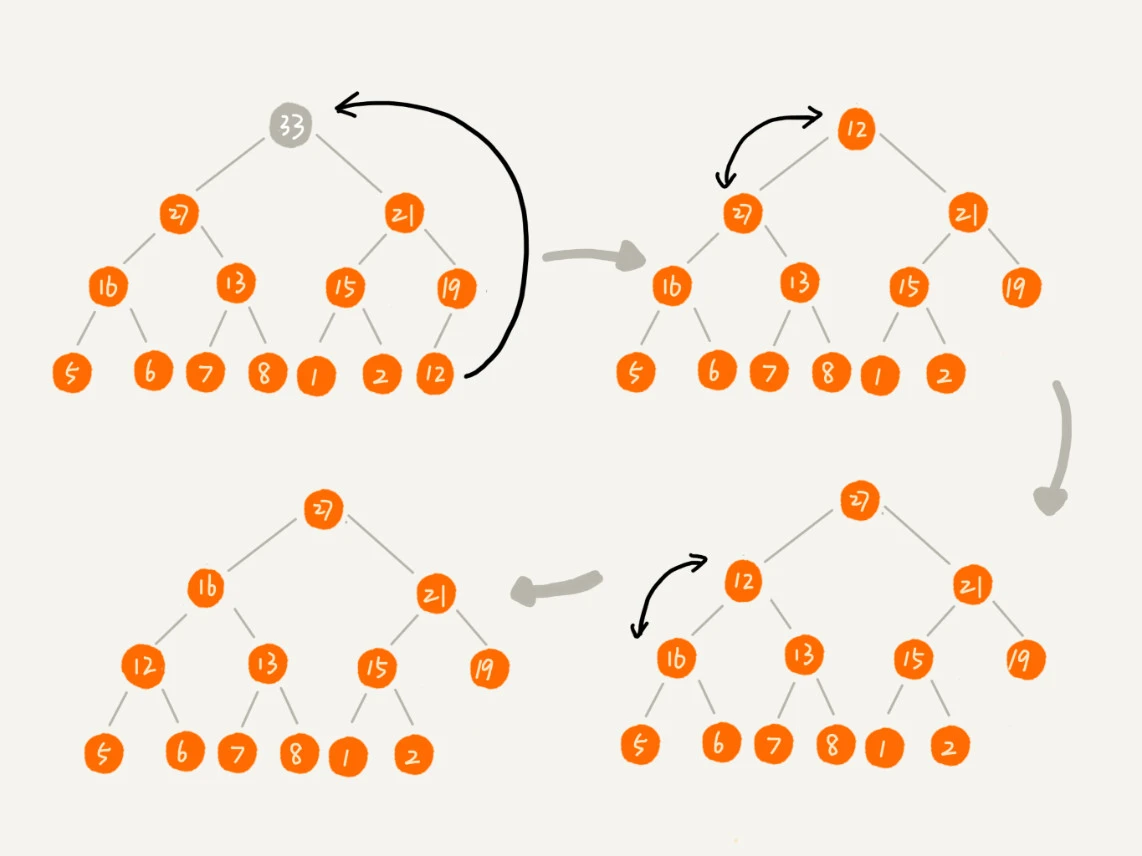 
代码实现如下：
public class Heap
{
private int[] _array;
private int _count = 0;
private readonly int _capacity;
public Heap(int capacity)
{
_capacity = capacity;
_array = new int[capacity + 1];
}
public void insertBulk(params int[] data)
{
if (data != null && data.Length > 0)
{
foreach (var item in data)
{
insert(item);
}
}
}
public void insert(int data)
{
if (_count >= _capacity) return;
_count++;
_array[_count] = data;
var index = _count;
while (index / 2 > 0 && _array[index / 2] < _array[index])
{
swap(index, index / 2);
index = index / 2;
}
}
public int deleteTop()
{
if (_count == 0) return -1;
var top = _array[1];
_array[1] = _array[_count];
_count--;
var i = 1;
while (true)
{
var maxPos = i;
if (i * 2 < _count && _array[i * 2] > _array[i]) maxPos = i * 2;
if (i * 2 + 1 < _count && _array[i * 2 + 1] > _array[maxPos]) maxPos = i * 2 + 1;
if (maxPos == i) break;
swap(i, maxPos);
i = maxPos;
}
return top;
}
private void swap(int index1, int index2)
{
_array[index1] ^= _array[index2];
_array[index2] ^= _array[index1];
_array[index1] ^= _array[index2];
}
}堆的应用
优先级队列
队列最大的特性就是先进先出。不过，在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。如何实现一个优先级队列呢？方法有很多，但是用堆来实现是最直接、最高效的。这是因为，堆和优先级队列非常相似。一个堆就可以看作一个优先级队列。很多时候，它们只是概念上的区分而已。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。
合并有序小文件
假设我们有 100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件。这里就会用到优先级队列。整体思路有点像归并排序中的合并函数。我们从这 100 个文件中，各取第一个字符串，放入数组中，然后比较大小，把最小的那个字符串放入合并后的大文件中，并从数组中删除。假设，这个最小的字符串来自于 13.txt 这个小文件，我们就再从这个小文件取下一个字符串，放到数组中，重新比较大小，并且选择最小的放入合并后的大文件，将它从数组中删除。依次类推，直到所有的文件中的数据都放入到大文件为止。这里我们用数组这种数据结构，来存储从小文件中取出来的字符串。每次从数组中取最小字符串，都需要循环遍历整个数组，显然，这不是很高效。有没有更加高效方法呢？这里就可以用到优先级队列，也可以说是堆。我们将从小文件中取出来的字符串放入到小顶堆中，那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。我们将这个字符串放入到大文件中，并将其从堆中删除。然后再从小文件中取出下一个字符串，放入到堆中。循环这个过程，就可以将 100 个小文件中的数据依次放入到大文件中。
求Top K
求Top K的问题可以抽象成两类。一类是针对静态数据集合，也就是说数据集合事先确定，不会再变。另一类是针对动态数据集合，也就是说数据集合事先并不确定，有数据动态地加入到集合中。针对静态数据，如何在一个包含 n 个数据的数组中，查找前 K 大数据呢？我们可以维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了。遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，时间复杂度就是 O(nlogK)。针对动态数据求得 Top K 就是实时 Top K。怎么理解呢？我举一个例子。一个数据集合中有两个操作，一个是添加数据，另一个询问当前的前 K 大数据。如果每次询问前 K 大数据，我们都基于当前的数据重新计算的话，那时间复杂度就是 O(nlogK)，n 表示当前的数据的大小。实际上，我们可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，我们就拿它与堆顶的元素对比。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。这样，无论任何时候需要查询当前的前 K 大数据，我们都可以立刻返回给他。
求接口99% 响应时间
我们维护两个堆，一个大顶堆，一个小顶堆。假设当前总数据的个数是 n，大顶堆中保存 n99% 个数据，小顶堆中保存 n1% 个数据。大顶堆堆顶的数据就是我们要找的 99% 响应时间。每次插入一个数据的时候，我们要判断这个数据跟大顶堆和小顶堆堆顶数据的大小关系，然后决定插入到哪个堆中。如果这个新插入的数据比大顶堆的堆顶数据小，那就插入大顶堆；如果这个新插入的数据比小顶堆的堆顶数据大，那就插入小顶堆。但是，为了保持大顶堆中的数据占 99%，小顶堆中的数据占 1%，在每次新插入数据之后，我们都要重新计算，这个时候大顶堆和小顶堆中的数据个数，是否还符合 99:1 这个比例。如果不符合，我们就将一个堆中的数据移动到另一个堆，直到满足这个比例。